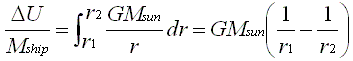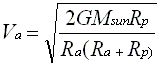On a separate topic, regarding Orion, adding a little more to the other
discussion referenced before seems worthwhile.
The VISTA ICF mentioned in the
Lawrence Livermore National Laboratory paper is one hypothetical form of external nuclear pulsed propulsion, what I usually call an Orion variant. If one has heard of the Daedalus starship proposal, that's also ICF. ICF stands for inertial (not internal) confinement fusion. The theoretical concept involves a simpler equivalent of a miniature thermonuclear bomb but with an external driver pulse replacing the fission trigger (and bulky chemical explosives), allowing the efficient yield to be smaller since there is no longer a minimum critical mass with no fission used. Optionally, it may be scaled down to a very miniscule fraction of a kiloton per pulse. The fusionable fuel of each target (pulse unit) is momentarily compressed and heated from all sides by the inertia of an imploding capsule wall, imploding due to being blasted by the external driver array, igniting, and then exploding from the resulting fusion energy release.
Pure-fusion ICF is the most technologically difficult nuclear pulse propulsion system but has advantages if it did one day become plausible.
An Orion propulsion system with pulse units using A-bombs or regular thermonuclear bombs has some disadvantages. For example, it requires a relatively high minimum yield per pulse, for reasonable efficiency, with the critical mass of the fission triggers. Politically, there are the obvious political complications of using nuclear bombs, much more so than using small fuel capsules imploded and ignited by an external driver. But it is the system based most on existing technology, with an example of some missions readily possible with such well worked out
some time ago.
Then there is mag-pulse Orion, e.g. this
Mini-Mag Orion. It much reduces fission critical mass and reduces the pulse unit complexity compared to stand-alone nuclear bombs. Small plutonium capsules can be imploded by a large external driver system to greater compression, density, and lower resulting critical mass than with chemical explosive implosion, with a driver still requiring a lot less performance than that required for ICF fusion.
And there is antiproton-catalyzed microfission/fusion, as illustrated by the
ICAN II concept. It is lesser in antimatter requirements than a pure-antimatter drive by a factor of enough millions to have a relatively good chance of being practical in the relative near-term foreseeable future. Again, it allows relatively low-yield pulses if desired.
For nuclear pulse propulsion in general, while starship concepts approach up to on the order of a million-sec specific impulse, that isn't even the goal for interplanetary transport, particularly not with the tradeoffs involved, and the average proposal for an interplanetary craft involves tens of thousands of sec Isp or less, along with usually <=~ 1g acceleration during periods of thrusting in deep space. That's substantial in today's perspective, compared to chemical rocket engines being a few hundred sec Isp; today's ion engines running off small solar panels like the
ion engine of the
DS1 probe accelerating it at around an 0.00002-g initial rate, taking a couple months for the first 1 km/s of delta v alone; and so on.
If politics prevented any nuclear-pulse-propulsion implementation, high-speed interplanetary transport market niches might be eventually satisfied by externally-powered propulsion, such as a sub-micron-thickness array of suitable high-temperature photovoltaic cells illuminated by a powerful laser at up to orders of magnitude greater intensity than natural sunlight. High efficiency is possible by matching the laser wavelength to the PV cells, unlike broad-spectrum sunlight. Such might obtain a power to weight ratio vastly above regular onboard power production, using instead the power beamed from large stationary installations millions of kilometers away. For example, while unlikely to provide minimum-cost bulk cargo transport, such might be like the Concorde of a space civilization for interplanetary passengers in a hurry.
However, by default, such tends to be relatively expensive per unit of energy involved, also with lesser delta-v capabilities compared to Orion variants.
◊◊◊◊◊◊◊◊◊◊◊◊◊◊◊◊◊◊◊◊◊◊


Topics like the delta-v to Pluto or the minimum delta-v to escape the solar system seem to have come up a lot in this thread.
Let's illustrate some of the complexity for calculating minimum delta-v to escape the solar system, plus some interesting possible "tricks."
In many cases, in order to do much calculation for a trip starting from earth orbit, one must consider earth's velocity around the sun,
which is 29.8 km/s.
Let's first illustrate how that affects the delta-v to escape the solar system, neglecting techniques like gravity assists for now.
If one unrealistically neglected orbital velocity and incorrectly treated a spacecraft as starting stationary 1 AU (
a distance of ~ 1.496E8 kilometers) from the sun, that would lead to calculations as follows:
F_gravity / M_ship = G * M_sun / (r^2), where G is the
gravitational constant of 6.67E-11 N * m^2/kg^2, while M_sun is the
Sun's mass of 1.99E30 kg; and
r is the distance from the sun.
Force * distance equals work (energy), so one can evaluate the difference in gravitational potential energy of ship's mass being at a distance r_1 from the sun versus it being at a distance r_2 from the sun with the following integration:
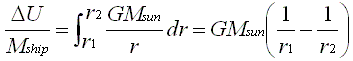
To find the amount equal to the kinetic energy for escape velocity from that location in the sun's gravitational field, set r_1 =~ 1.496E11 meters for 1 AU from the sun and r_2 to approach infinity. So the ship starting 1 AU from the sun needs 887 MJ of energy of kinetic energy for each 1 kilogram of its mass to depart the solar system, to obtain escape velocity from its starting position. Kinetic energy is KE = 0.5 * M * V^2, so that corresponds to ~ 42.1 km/s delta v.
Such is the nominal minimum delta-v for a ship to escape the solar system if starting 1 AU from the sun ... if the ship unrealistically starts as stationary with respect to the sun. To illustrate how the math works, if one instead substituted into the preceding integral a value of 6.96E8 meters for an imaginary ship starting on the surface of the sun, considering
sun's radius, that nominal delta-v would become 618 km/s. Such suggests how there were no careless mistakes in derivation, as it appropriately matches the figure
that is the sun's escape velocity.
The preceding math was fine in itself.
But is 42.1 km/s delta-v really the minimum involved in a real-world craft departing the solar system from 1 AU away from the sun? Not at all.
The math is only as good as the starting assumption, which is unrealistically treating the ship as starting from 0 km/s relative to the sun.
The problem is neglecting how a ship departing earth orbit or elsewhere would actually start with orbital velocity around the sun. No ship would really start just suspended in space stationary with respect to the sun while being 1 AU from it.
Let's now illustrate for a ship that starts in a solar orbit 1 AU from the sun (e.g. following several million kilometers behind earth). For an approximately circular orbit, it is currently orbiting the sun at 29.8 km/s. What happens if a burst of thrust from its engines gives 12.3 km/s delta v with that velocity in a directional parallel to the original orbital velocity, such that the ship reaches (29.8 + 12.3) km/s or thus 42.1 km/s relative to the sun? It eventually escapes the sun's gravity, departing the solar system.
Observe how different 12.3 km/s is from 42.1 km/s, illustrating the major effect of taking into account the starting orbital velocity.
Actually, even the 12.3 km/s figure is only valid for the ship starting in a solar orbit 1 AU from the sun without starting significantly within earth's gravity well, not for a ship in earth orbit, nor for an object starting on earth's surface.
Let's now illustrate for an object starting from earth's surface, such as a high-velocity mass-driver projectile that for some reason one wants fired at such velocity to leave the solar system. Assume it is launched in the right direction, which is quite important, as will be discussed later. One wants it to have 12.3 km/s additional velocity beyond earth's 29.8 km/s orbital velocity around the sun for 42.1 km/s total velocity relative to the sun.
That means it should have 12.3 km/s velocity relative to earth left over after escaping earth's gravitational field.
Earth's escape velocity
that is 11.186 km/s corresponds to 62.56 MJ/kg being taken from the projectile by earth's gravitational field. If the projectile is to have 12.3 km/s velocity left over afterwards, it needs to have 75.6 MJ/kg left over afterwards (of kinetic energy relative to earth). So, aside from atmospheric drag losses, it needs to start with ~ 138.2 MJ/kg, which means 16.6 km/s velocity. One may note that is not the same as (12.3 + 11.2) km/s, not 23.5 km/s. If a projectile goes at 16.6 km/s just above earth's atmosphere, headed in the right direction, it can escape the solar system even after losses going out of earth's gravity well.
One can indirectly double-check that there weren't careless mistakes in the preceding calculations by comparing to the following, which implies the same:
C. Park & S.W. Bowen wrote:Ablation and deceleration characteristics are analyzed for a hemisphere-cylinder-shaped projectile protected by a graphite nose tip and launched vertically upward with a velocity in excess of 17 km/sec. It is shown that ablation and deceleration of the projectile are in tolerable ranges for a scheme in which such projectiles are packed with nuclear wastes and launched with a mass driver to dispose of nuclear wastes outside the solar system.
[...]
If the projectile survived the atmospheric flight and had a velocity when above the atmosphere greater than 16.6 km/s, it would escape the solar system, provided the launch was properly timed and aimed [e.g. launched vertically at dawn from the equator].
AIAA 1981-355
In the preceding, why does the launch have to occur at around a particular time to minimize velocity requirements?
It is because direction matters much, the right trajectory being practically necessary for this.
For example, suppose the vertically-launched projectile was fired at the worst time 12 hours different from the best time, so the velocity given to it by the launcher was directed opposite to earth's orbital velocity around the sun instead of parallel to it.
In that case, instead of eventually 12.3 km/s added to earth's 29.8 km/s orbital velocity for 42.1 km/s velocity, the situation would become 12.3 km/s subtracted from earth's orbital velocity. The projectile would drop to 17.5 km/s relative to the sun, moving slower than earth.
In that case, the projectile would end up in a highly elliptical orbit around the sun. Any elliptical solar orbit is like this:
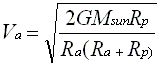
In the preceding, V_a is the aphelion velocity, which is the velocity at the greatest distance from the sun. In this case, that aphelion velocity is now 17.5 km/s. M_sun and G are the mass of the sun and the gravitational constant respectively again. R_a is the aphelion distance of 1 AU.
R_p is the new perihelion distance that is now going to be a lot closer to the sun than 1 AU. With respect to the sun, this projectile fired "backwards" in the wrong direction lost a lot of velocity compared to earth's orbital velocity.
Specifically, in this case, R_p =~ 3.12E10 m or 0.21 AU.
As the projectile "falls towards the sun" on its new orbit, it reaches a perihelion velocity of 83.9 km/s relative to the sun at its close point of 0.21 AU. That is a velocity subsequently lost as it moves back away from the sun later in its elliptical orbit, moving back out towards 1 AU aphelion.
As another illustration, one may look at dropping nuclear waste into the sun. Such is an idea sometimes suggested by individuals in the general public unfamiliar with orbital mechanics. To "drop into the sun" an object starting from earth's vicinity, it needs delta-v negating nearly all of earth's 30 km/s orbital velocity around the sun. Otherwise, the object merely ends up an elliptical orbit passing closer to the sun without intercepting the sun itself (the sun's radius being such that its surface is 7E5 kilometers from its center).
As previously implied, even escaping the solar system actually takes less delta-v. When starting at 30 km/s relative to the sun at 1 AU distance, it is easier to rise by 12 km/s to reach 42 km/s than to drop by about 30 km/s to reach about 0 km/s. That's why the preceding nuclear waste disposal paper suggested sending the projectiles on a trajectory escaping the solar system instead of sending them into the sun. (That's not to say that the trouble of either option is really at all necessary for waste disposal, just that the former is energetically easier than the latter).
Incidentally, although topics like orbit calculations are mainly covered in textbooks, one of the better online discussions is
here.
Now, what about a craft starting in low earth orbit that is to escape the solar system? Its altitude is low enough that the situation is like starting from earth's surface aside from the 7.9 km/s LEO orbital velocity around earth. If it is to obtain solar system escape velocity, one again wants 16.6 km/s velocity (parallel to earth's orbital velocity) relative to earth, for the velocity when it is close to earth.
So the craft needs ~ 8.7 km/s delta-v if it does a quick engine burn parallel to its LEO orbital velocity around earth. That's for such being done at a time close to earth and in a direction parallel to earth's orbital velocity around the sun.
In contrast, if the craft did an engine burn of ~ 3.3 km/s to reach earth escape velocity from LEO orbit, drifted slowly several million kilometers out of earth's vicinity, thus becoming almost stationary with respect to earth and 29.8 km/s relative to the sun, then there would be an undesirable 12.3 km/s involved in reaching the solar system escape velocity at 1 AU of 42.1 km/s total velocity. The burn in LEO described previously is a better way, in part for reasons related to those involved in the Oberth maneuver described later.
Also, all of the discussion so far is neglecting the option of gravity assists, described later.
For the direct route without gravity assists, an example is that a 450-sec specific impulse (4400 m/s exhaust velocity
v_e) chemical rocket starting in LEO would have an initial to final mass ratio of about 7.2 to 1 for escaping the solar system.
The calculations is straightforward as one knows the 8.7 km/s delta-v involved from the previous discussion, substituting it into the rocket equation
that is change_in_velocity = exhaust_velocity * ln (m_initial/m_final), where ln is the natural log.
The rocket equation can be rewritten as m_initial / m_final =
e^(∆v / v_e), where
e =~ 2.71828.
However, rather than the "direct route" really being fully applicable to historical deep-space missions with chemical propulsion, the technique of gravity assists has been used instead. No historical missions have actually involved having to deliver 8.7 km/s delta v in LEO, only much less.
For example,
the probe Voyager 1 launched back in 1977 is currently 15 billion kilometers from the sun, beyond the orbits of the planets, on the way out of the solar system, traveling at 17 km/s velocity relative to the sun. That was not obtained by it having had as much propellant mass as one would expect if not for gravity assists. Indeed, the delta-v capacity directly from its chemical propulsion was rather limited. But
Voyager 1 used multiple gravity assists, taking advantage of how planets move fast around the sun while having gravitational forces tugging any object that passes close nearby. A little like bouncing off a giant moving billard ball but with a gentle gravitational tug swinging past a planet rather than destructive physical contact, gravity assists are useful for low-performance craft like chemical rockets; one description is the NASA educational page
here, which includes an analogy:

In such a manner, much less than 8.7 km/s delta-v beyond LEO is nominally sufficient for the amount of actual engine performance needed to leave the solar system or fly by locations in the outer solar system.
However, arranging repeated gravity assists after waiting for planets to get into the right locations for where one is headed is a slow process. For example,
Voyager 1 did it over a period of years.
Because of the limited few km/s of delta-v deliverable with the gravitational fields of the planets and the time involved in going off to perform gravitational assists, such are less likely to be used as much with spacecraft having much higher performance engines. But they are useful if minimum delta-v for traveling to the outer solar system is the priority.
With enough gravity assists, one can eventually get anywhere in the solar system even with chemical propulsion, in the manner of some of NASA's historical space probes going as far as Neptune and beyond. However, such is very slow. (Such also requires a relatively substantial ratio of propellant to payload in LEO even just for getting on its initial trajectory despite the small number of km/s delta v involved, with the low Isp of chemical rocket engines). A vastly higher-performance propulsion system such as Orion variants and some other options would work much better if one doesn't want to spend years just getting to the outer solar system.
A different technique with some potential applications is the principle of the Oberth maneuver, for craft with engines having suitable thrust capabilities:
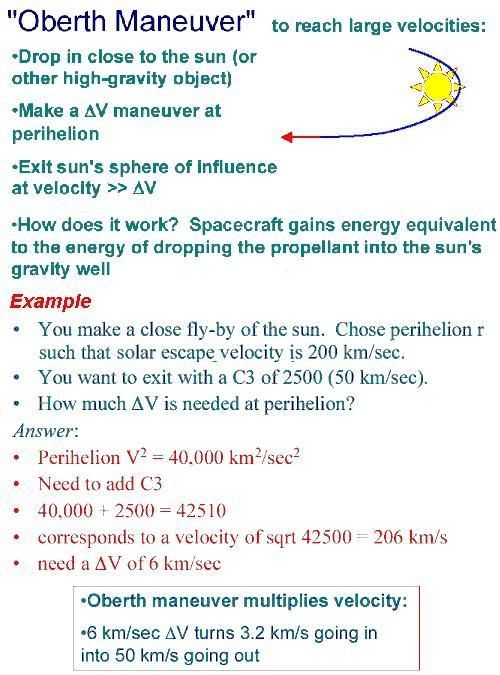
Click on the above image for the source of its description, a PDF file that is quite a good presentation about a number of topics.
The above figures are just one illustration. The situation for an Oberth maneuver with the sun depends on the delta-v capabilities of the ship and on how close it flies to the sun.
The latter is restricted by the ship's delta-v for lowering its perihelion and by its ability to avoid getting fried, its heat resistance.
Under some assumptions, the Oberth maneuver it is quite helpful up to hundreds of km/s velocity left over after exiting the sun's gravity, for a ship with a fraction of that in delta-v provided by its engines and the ability for a close solar fly-by. That's too little to help a starship much, but it is a possibility for helping speed transport to the outer solar system and a bit beyond.
Compared to the more pedestrian gravity assist technique, the Oberth maneuver requires more delta-v to properly arrange, but it is applicable to a lot more km/s gain, with a solar fly-by able to give tens to hundreds of km/s effective extra delta-v under some assumptions.
Gravity assists have been important to historical chemical-propulsion space probes. In contrast, for example, higher-performance interplanetary Orion craft would tend to obtain proportionally less benefit from gravity assists, less likely to spend the time, since a small number of km/s matters less to them, but they could be more capable of using the Oberth maneuver for more "free" km/s gain if headed for the outer solar system, Kuiper Belt, or Oort Cloud.
The Oberth maneuver is curiously reminiscent of Star Trek IV's "slingshot around the sun," minus the unrealistic time-travel and warp drive.