brianeyci wrote:I believe exact's used in science it means with such a high degree of accuracy and precision that you cannot with your instruments find any experimental error. I'm sure you already know this. Since I can tell with my eye that the thing isn't exact, it's not (the puzzle, not your cutouts).
This reminds me of an Engineering joke my Calculus teacher told me. Two men die in a car crash, one is a Mathematician, one is an Engineer. St. Peter says they may see their dead wives, but they may only walk to them by crossing half the distance between them and the wife each time. The Mathematician dispairs and cries to St. Peter "But I will never reach her! How can you be so cruel?". The Engineer walks the distances and easily reachs his wife, then turns to St. Peter and the Mathematician and shrugs. "Close enough" he says.
13cm with a straightedge and pencil means that you draw a line that anyone with a straightedge can measure to be 13cm.
I guess I approach always from a math angle.
Heh, that's a good pun.

Why do you quote neat? It's because you know that it's not really neat, that it's not really exact. I still think the most straightforward answer is that the pieces are not exact, or not accurate enough, given the context of the grid implying exactness. You don't need math to tell this--you can just eyeball it.
Saying that rearranging the pieces is the answer is missing the whole point of the "trick", that's why I think it's wrong.
Brian
"Neat" as in "interesting", not as "neat" as in "clean".
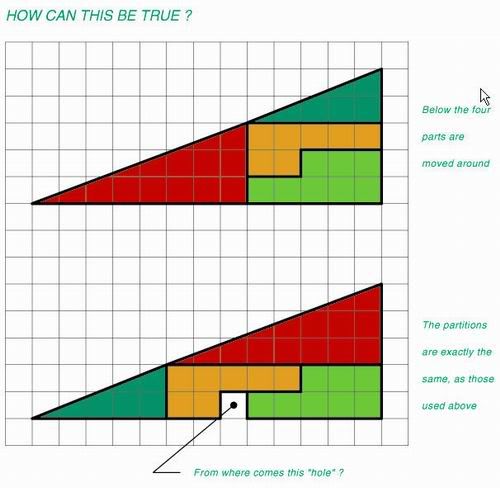
But remember, the above or the cutout I made aren't science or math. In fact, the puzzle seems designed specifically to those who overanalyze the situation. Surlethe originally was confounded because the thing didn't make any mathematical sense. You can approach it mathematically, of course, but it is very simple to say that when you move the red block to the top corner of the triangular arrangement, in order to maintain the general shape of the arrangement you are left with a rectangle under the the red triangle that is 8 by 2 units. You can make a rectangular arrangement of shapes with the two "L" pieces matching those diminsions, but you are left with the hole. Hence, the hole comes from the different configuration of the "L" pieces in the total triangular arrangement.
If anything about the above is untrue, feel free to point it out. However, the key to the puzzle is to not walk into the trap of overthinking it. It asked you a simple question, and has a answer so simple that most people just overlook it.