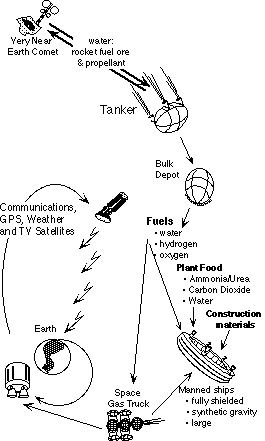
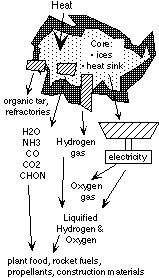
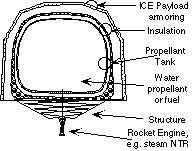
TheLemur wrote:Kuroneko provides the key equation:
P = Fu/2
where P is the power (in terms of energy input into the engine per second, by way of fuel or what have you),
Why do you assume the power is fixed?
Power is variable, up to a point. At this point, the engine is absorbing so much heat from the exhaust that, in order to maintain sufficient thermal conduction, the walls have to be at the melting point... which is not good.
TheLemur wrote:Obviously if you're burning fuel at twice the rate, you're going to get twice the power. This makes sense for an ion engine or other engine with a fixed, external power source, but for Orion the power is provided by the bombs themselves.
If you increase bomb rate, you of course increase thermal and mechanical stress on the pusher plate. Eventually, given some level of technology and ship mass, the plate's gonna fail. Any given Orion engine will a maximum practical bomb rate, beyond which the pusher plate breaks down so fast that you will not be able to complete your mission. This, of course, limits the amount of power availible.
You seem to imagine that you can just increase power consumption of some kind of engine indefinitely. You cannot. With any engine, there will be a limit to how much power you can give the exhaust.
TheLemur wrote:Essentially, we made different assumptions; you assumed fixed power and fuel mass, I assumed fixed delta-V and exhaust velocity.
And of course, delta-V is a
function of how long you burn your engines, which is the point at issue — how long do you burn your engines to minimize time?
Given my assumptions are sensible and yours aren't, I believe my conclusion.
TheLemur wrote:that spacecraft would be able to reach Pluto in 16 years, 4 months (delta-V = 28.21 km/s, enough to escape the solar system)
Could you please go into further detail on this calculation? What trajectory are you taking and what assumptions are you making?
That the dry weight of the mission can be brought down to 26 kg (the rest of 367 kg is propellant — hey, it's sci-fi), that the ion engine has a battery made by the MONDO Company, able to power the ion engine throughout the trip, and the engine has a thrust of 20 mN at a specific impulse of 3100 seconds. All of these I've stated. Also, I assumed no gravity and a trip distance of 7.3 billion km, and the mission is a flyby.
The acceleration of the craft is no less than 20 mN/367 kg = 5.45e-5 m/s. Take the familiar D = at²/2 and solve for t, which you get 5.176e8 seconds, which is about 16 years and a bit. Multiply acceleration by flight time to get the change in velocity: ∆v = at = 28.21 km/s. This is lowballing; the acceleration is an increasing function of time.
To get propellant consumption, find the exhaust velocity, which is specific impulse multiplied by 1 G, here u = 30.38 km/s. A chunk of the craft's mass (propellant), ∆M, is thrown at exhaust velocity u for a gain in momentum ∆p = u∆M. The increment of momentum per increment in time ∆t is ∆p/∆t = u ∆M/∆t, and if we let ∆p/∆t become infinitesmial, it becomes dp/dt = u dM/dt. dp/dt is of course, thrust (force). So 20 mN = u dM/dt -> dM/dt = 20 mN/(30.38 km/s) = 6.58e-7 kg/s. Multiply by the number of seconds and you get 340.75 kg, which is lower than the beginning mass of the mission by about 26 kg.
I could continue, making acceleration a function of mass, and therefore time using the fuel consumption to get a distance as a function of time with the functional acceleration, but that was a bit too much for so late at night. Please note that because of the increasing acceleration, time will be reducd.
TheLemur wrote:Yes, they'll begin tight, but they will slowly straighten out as the spacecraft climbs out of the planet's gravity well.
This is a *bad* thing, because acceleration is most fuel-efficient at high velocities and big circular orbits have low velocities.
Did you flunk high school physics, or have you not just taken it yet? The amount of kinetic energy you have to expend to accelerate is independent of your initial speed.
TheLemur wrote:Why do think SMART-1 used its thrusters only at perigee?
Because it wanted
specifically to get into a lunar transfer orbit, which would minimize the delta-V needed? I did say that orbit considerations are important if you want to get to a specific destination, did I not?
TheLemur wrote:This is true. However, if you add 1 m/s to an object in LEO, and then 1 m/s to an object in LEO+1km, and then 1 m/s to an object in LEO+2km, etc., even if you still add the full 8 km/s, you're not going to escape the solar system, because at a certain point you will escape from the Earth's gravity with almost zero additional velocity and wind up in solar orbit, from which it takes a minimum of 12 km/s to escape onto a hyperbolic trajectory.

Did you get your celestial mechanics degree out of a cracker jacks box? C'mon! Make more shit up. I could use a laugh.
TheLemur wrote:Yes, but it also requires no fuel other than the power source. Did you forget about that part? An ion engine trying to accelerate to relativistic velocities will run out of fuel very quickly; a photon engine will not.
Neither will the power source, I see. Oh, wait; It will.
And stop moving the goalposts, fucktard. One of your requirements for "better engines" was "higher thrust than ion engines." Photon engines do
not fit this critera.
TheLemur wrote:
I consider an engine type as having been "proven to work" when we have an example of a system flying and working. "Almost" only counts horeshoes and handgrenades. Ion drives have the highest specific impulse of those proven engines.
Then your 260 km/s Earth-to-Pluto example is bunk, because we've only flown ion engines with a specific impulse of a few thousand seconds.
If you want. (It was 231 km/s, BTW.) It was a gedanken experiment, anyway, assuming that we can spiffy up the ion engine to high but not completely outrageous figures. My point still stands: ion engines have the highest specific impulse of the proven engines.
PS, even
I know that your spew is not what Ender meant by "breaking down".