Calculating Acceleration: what am I doing wrong?

[Junghalli]

I got this formula for acceleration from Atomic Rockets.

Acceleration (m/s) = thrust (newtons) / present mass (kg)

So I tried plugging the thrust and mass for the Daedalus spacecraft into it. The Wikipedia page says it the first stage has a thrust of 754,000 N, a propellant mass of 46,000 tons, and a payload of 6,670 tons (including second stage propellant).

754,000 / 52,670,000 = .014 m/s^2

754,000 / 6,670,000 = .113 m/s^2

The problem is that the Daedalus first stage has a delta V of 21,285 km/s (7.1% c) and a burn time of 2.05 years, and it couldn't possibly achieve that with these accelerations. .113 m/s^2 for 2.05 years is 7,305 km/s, and that's how fast it would be accelerating at the end of its burn time, after it had already lost most of its mass. Obviously, something is kooky here.

I doubt the Atomic Rockets equation is wrong, and I can't really see how I'm messing it up (it's pretty damn self-explanatory). I suspect the Wikipedia page got the thrust wrong and it's actually 7.54 MegaNewtons. An acceleration of .14 m/s^2 going up to 1.13 m/s^2 gives figures much more in line with the actual mission. Unfortunately I haven't been able to find any figures on Google besides the impossible 754 KN one, anybody out there have any other numbers?

Just wanted to check this with you guys and make sure I'm not making any mistakes.

[Wyrm]

Delta V is properly calculated by

∆v = ∫ |a| dt

Acceleration, however, is a function of time (due to mass loss) so you have to calculate a rate of fuel consumption. 2.05 years is 6.4691696693e7 seconds, so 46,000 tonnes over that time is 7.1106497977e-1 kg/s, so

a(t) = (754,000 N)/[(5.267e7 kg) - (7.1106497977e-1 kg/s) t)]

Doing the integration from 0 to τ=(6.4691696693e7 s), we get

∆v = (7.1106497977e-1 kg/s)(754,000 N) log[(5.267e7 kg)/{(5.267e7 kg) - (7.1106497977e-1 kg/s) τ}]

But {(5.267e7 kg) - (7.1106497977e-1 kg/s) τ} is simply the final mass, 6.670e6 kg, so the ∆v = 1.1078999171e6 m/s. In other words, about an order of magnitude and a third smaller than the stated delta v.

Yea, the thrust is too small. Or the mass too big.

[Wyrm]

Ghetto Edit: Damn. Did the calc wrong. I realized that the front factor has the wrong units during dinner. Here's the corrected factor:

(754,000 N)/(7.1106497977e-1 kg/s)

which has units of speed, and gives us a final delta v of ∆v = 2.1911996501e6 m/s. Oh well. Wikipedia still fucked up. Go fig.

[Junghalli]

Well Wyrm, it embarasses me to admit my eyes sort of glazed over there a bit, I'm not exactly what you'd call a math person.

The reason I ask this is because I'm writing a little essay on realistic space combat for the Tech forum on SB, and I'm really just trying to get a feel for what sort of accelerations are realistic for high-performance drive systems. I've been just using the thrust numbers here so far, but it doesn't have an estimate for Daedalus (it does give a number for ICF max, but given that ICF is limited by the need to not melt the bell I'm betting that isn't very realistic).

It looks so far like with the best drives you're talking accelerations in the range of a few G for very small ships (dozens of tons), a few m/s^2 for ships in the low thousands of tons, and fractions of m/s^2 for ships of tens of thousands of tons. For a high-endurance "torchship" you're probably talking about fractions of m/s^2 for a fully fueled ship and a handful of m/s^2 for a "dry" ship.

Is that about right? Or am I off base? I remember somebody mentioning a 10,000 ton Orion could get up to 4 G, but plugging the given thrust for Orion MAX into A = F/M only gives .8 m/s^2.

[Junghalli]

Alternately, one go by the estimate that a 10,000 ton Orion can get up to 4 G and work off that. A ship 4 times heavier should take 4 times as much energy to accelerate, I'd think, so say if you have a 10,000 ton ship with 30,000 tons of fuel it should be able to get 1 G when fully fueled and 4 G when running on fumes.

I wonder if a NSWR would have the same performance. It is the same basic principle as Orion, and much more efficient. Then again, I believe it has some overheating problems with the nozzle.

[Surlethe]

If it's a multi-stage rocket, won't you have to split the integral to take into account the stage separation and the discontinuity in acceleration because of that?

[fnord]

Surlethe, I think Junghalli is worrying only about the first stage of the damn thing. Second stage is still payload.

junghalli, do you know what exhaust velocity the design proposed to use?

[Sikon]

Acceleration (m/s) = thrust (newtons) / present mass (kg)

Yes. Force is mass times acceleration. F = ma while a = F / m. Newton's second law.

The Wikipedia page says it the first stage has a thrust of 754,000 N

Not sure about that. A different description:

Alan Bond and Anthony R. Martin’s summary paper “Project Daedalus: The Mission Profile.” The baseline vehicle finally arrived at (after various alterations along the way) looked like this:

Propellant mass first stage: 46,000 tons
Propellant mass second stage: 4000 tons
First stage mass at cutoff: 1690 tons
Second stage mass at cutoff: 980 tons
Engine burn time first stage: 2.05 years
Engine burn time second stage: 1.76 years
Thrust first stage: 7.54 x 10^6 N
Thrust second stage: 6.63 x 10^5 N
Payload mass: 450 tons

I remember somebody mentioning a 10,000 ton Orion could get up to 4 G, but plugging the given thrust for Orion MAX into A = F/M only gives .8 m/s^2.

Different Orion concepts have different thrust to weight ratios depending upon the design for a particular mission. There's a tradeoff between specific impulse and thrust with any real-world concept for high-performance engines, as will be discussed more later.

The ground-launched interplanetary Orion variant (10000 tons) would need well above 1g (10 m/s^2) acceleration, of course. Peak g forces for the passengers from the detonation pulses are higher than the average acceleration. One design had the shock absorbers limit those to 4 g's. Another design had it less bumpy for the humans with closer to 2 g's.

It looks so far like with the best drives you're talking accelerations in the range of a few G for very small ships (dozens of tons), a few m/s^2 for ships in the low thousands of tons, and fractions of m/s^2 for ships of tens of thousands of tons.

What is possible does not vary with the size of the ship to that degree. For example, if a 1000-ton engine has a maximum thrust to weight ratio of 6 at a particular specific impulse, a 2000-ton ship with 50% of its mass in the form of such an engine could accelerate at 3g. Or a 20000-ton ship could also accelerate at 3g if it had 50% of its mass in the form of ten 1000-ton engines or a single 10000-ton engine with about the same thrust-to-weight ratio.*

* (Some engine concepts dependent on the surface area of thermal radiators as a limit would have less power dissipation per unit mass with increasing size, but, in that case, it is scaling to the 1/3rd power rather than linear scaling; each doubling of mass then would not halve surface area per unit volume but only decrease by 20% per doubling, all else being equal).

Of course, eventually a larger ship would become limited in acceleration. But that's not as much a problem for the size range relevant here. Both a 500-ton ship and even a 50,000-ton ship can have structure capable of withstanding even multiple g's of acceleration, although the same wouldn't be true for a 50-quadrillion-ton ship.

(That's like how a steel or titanium structural member with a few hundred MPa strength can withstand many times its own weight whether it is 5-meters or 50-meters long, though if one tried to make it kilometers long there would be a problem).

Rather, at high Isp, what usually would determine obtainable thrust-to-weight ratio is not so much the ship's structure but rather the power limit for not melting or overheating the engine, which is influenced by the exhaust velocity.

At constant power, there is a tradeoff between exhaust velocity and thrust.

Both small and large ships become limited to a small fraction of 1g acceleration if the priority becomes maximizing exhaust velocity.

Have extreme exhaust velocity and the ratio of kinetic energy to momentum for the exhaust becomes extreme. That means a small number of newtons of thrust per gigawatt of engine power. Since any realistic engine can't withstand an arbitrarily high number of gigawatts per unit mass without melting, it must have low thrust-to-weight ratio if it has extreme specific impulse (Isp).

To use a very rough analogy, think of an aircraft on earth. Its engine causes an exhaust of air going at a few hundred m/s. The ratio of kinetic energy to the momentum for such low exhaust velocity is not high, so there's a lot of thrust obtainable per kilowatt of engine power. Now, imagine that same aircraft engine ran a generator that powered a spotlight with the same power. The recoil or thrust from the spotlight would be almost zero, being like a giant flashlight.*

* (The momentum to energy ratio of a photon from a flashlight isn't quite the same as that of a high-velocity particle of matter exhaust, but the approximate analogy is close enough: High enough exhaust velocity does make the momentum to energy ratio become far closer to that of photons than it was at low velocity).

For the most extreme situation, increase exhaust velocity towards the speed of light, and the drive becomes almost like a giant flashlight in terms of having an extremely low ratio of momentum to the enormous kinetic energy of the exhaust.

Or consider a less extreme situation. Suppose one has a nuclear-pulse propulsion drive massing X that can handle Y gigajoules of energy release per second detonating an appropriate distance behind the engine. If each pulse unit is surrounded by very little inert propellant, the exhaust velocity of its vaporized debris will be high, allowing high specific impulse, but momentum will be relatively low.

However, suppose one puts 100 times the mass of inert propellant around the pulse unit. Since kinetic energy equals 0.5 mv^2, the average exhaust velocity will be about 1/10th as much for about the same number of joules of total KE in the detonation. But momentum equals mv, so 100 times the exhaust mass with 1/10th the velocity gives 10 times the momentum per detonation.

By adding inert propellant, one can increase the thrust to weight ratio of the engine without exceeding its survivable power to mass ratio, yet such also causes the tradeoff of lower specific impulse.

In interplanetary applications where there's no need for starship-level Isp but higher acceleration is preferable instead, real-life proposals for nuclear pulse propulsion craft intentionally use a lot of inert propellant.

Example:

In the ICAN II concept paper here, as analyzed in a post here, each pulse unit involves 0.8 kilograms of inert propellant but a mere 0.003-kg nuclear fuel target (helped for ignition by a few billions of a nanogram of antimatter).

Such a large ratio of inert propellant to nuclear fuel mass much reduces exhaust velocity. The engine has only 13500 sec Isp in that particular case, even though more than an order of magnitude higher Isp is obtained by some other nuclear propulsion concepts.

But the specific impulse is still sufficient for the interplanetary mission. The engine gets an acceptable thrust to weight ratio (still low by sci-fi standards but ok for its mission), while its waste power is low enough to be handled with the help of a moderate-sized radiator circulating liquid droplets.

Another example of the tradeoff:

The U.S. Lawrence Livermore National Laboratory (LLNL) published a paper on a VISTA inertial confinement fusion engine concept. Here's a table from page 136 of the online document, and observe the tradeoff where higher exhaust velocity means lower acceleration to avoid exceeding the amount of thermal power that the engine can survive:



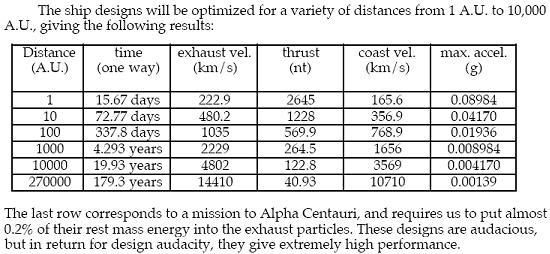
Whether a giant starship or the 3-ton interstellar probe illustrated in the above table, only low acceleration is possible when one seeks extreme exhaust velocity. Interplanetary ships can be high acceleration but not starships.

The exact figures would depend upon the engine technology and design. Some engines can handle more gigawatts of thermal power per unit mass than others. The best future nuclear pulse propulsion engine could be either better or worse performance than the example of the above table.

Very high exhaust temperatures can be handled due to limited heat transfer from the momentary duration of each pulse. (As a very rough analogy, part of the trick of nuclear pulse propulsion is like having one's hand in a hot oven for only a microsecond every second to limit heat transfer instead of holding it in there the other 99.999+% of the time).

But the general trend is that there is a tradeoff between exhaust velocity and acceleration for any high-performance engine, because nothing made from any element in the periodic table can withstand more than a limited amount of power per unit mass, even though concepts can use techniques like low duty cycle pulse operation, magnetic nozzles deflecting charged plasma away from the engine itself, etc.

[Junghalli]

Surlethe, I think Junghalli is worrying only about the first stage of the damn thing. Second stage is still payload.

Yes, I'm only looking at the first stage thrust and treating the entire second stage as payload.

junghalli, do you know what exhaust velocity the design proposed to use?

10,000 km/s

Not sure about that. A different description:

Alan Bond and Anthony R. Martin’s summary paper “Project Daedalus: The Mission Profile.” The baseline vehicle finally arrived at (after various alterations along the way) looked like this:

Propellant mass first stage: 46,000 tons
Propellant mass second stage: 4000 tons
First stage mass at cutoff: 1690 tons
Second stage mass at cutoff: 980 tons
Engine burn time first stage: 2.05 years
Engine burn time second stage: 1.76 years
Thrust first stage: 7.54 x 10^6 N
Thrust second stage: 6.63 x 10^5 N
Payload mass: 450 tons

Ah yes, I thought it would be 7.54 million newtons.

Of course, eventually a larger ship would become limited in acceleration. But that's not as much a problem for the size range relevant here. Both a 500-ton ship and even a 50,000-ton ship can have structure capable of withstanding even multiple g's of acceleration, although the same wouldn't be true for a 50-quadrillion-ton ship.

Rather, at high Isp, what usually would determine obtainable thrust-to-weight ratio is not so much the ship's structure but rather the power limit for not melting or overheating the engine, which is influenced by the exhaust velocity.

Yes, the thermal limitations are chiefly what I'm worried about here. I'm aware of the problems inherent in a high delta V and high acceleration, which is why I think space militaries would probably be mostly interested in drives like Orion or NSWR that move the energetic propulsive reaction outside the ship. I'm trying to determine what's reasonable for a drive system like that.

[kinnison]

Bussard put a little teaser at the end of his original article on Polywell electrostatic-confinement fusion, to the effect that (assuming the concept works in the first place) the design won't need much tweaking to make the fusion product nuclei go mostly in one direction when they are coming out. In other words, a fusion rocket.

One advantage of this setup is that the fuel can be chosen so as to produce very few neutrons - radiation is a serious concern in nuclear rocket designs. The most likely variant to manage this is protons reacting with boron-11; because there is too much energy release, most of the products will be alpha particles rather than carbon nuclei.

My physics is a bit too rusty to do the calculations, but the exhaust velocity would be a large fraction of the speed of light, as the exhaust is alpha particles carrying several MeV.

Incidentally, boron-11 is about 80% of boron atoms and hydrogen-1 is of course just about all of hydrogen, so it's conceivable that the fuel wouldn't even need isotopic separation. And boron is about four times as common as uranium, and isn't radioactive.

So; fusion motors might be the best option here. Also, as there is no physical contact between fusion plasma and the engine walls (not true for Orion designs) there might be less in the way of wear problems, too. The only problem I can see is that a fusion motor wouldn't have very high thrust, and hence couldn't be used to lift off - but do you really want a fusion motor running in atmosphere anyway? Remember the Kzinti Lesson.

[Junghalli]

Would that be a fusion fragment rocket you're thinking of? I've heard of it but I believe it's supposed to be a high efficiency low thrust system from what I've heard, so it'd probably be better suited to explorers than warships.

I'd say high thrust actually is rather desirable for a warship: it translates into higher acceleration, and hence higher tactical speed. There are some definite benefits to this, such as the fact that missiles will have a longer effective range against ships with lower acceleration (because the effective range will be determined by how much room the enemy ship needs to exceed the missile's delta V on the optimal possible escape vector).