Help setting up a double integral

[Aranfan]

So in my multivariable Calc webwork, I have the following question:

A cylindrical drill with radius 4 is used to bore a hole throught the center of a sphere of radius 5. Find the volume of the ring shaped solid that remains.


Being the idiot that I am, I can't figure out how to set this up as a double integral. So I used washers instead. I got 88pi/3.

The computer says this is wrong, so I figure before I email the teacher about a problem, I should try it with double integrals first. So I'm asking SD.net how I go about setting up the problem. Once it's set up I can evaluate it myself, but I can't figure how to set up the damn problem.

[Xenophobe3691]

X goes from 4 to 5, y goes from 0 to sqrt[x^2 - 5]?

[Aranfan]

Kay, but what gets integrated? What gets put in between the SS and the dA

[Wyrm]

For simplicity, let's work in cylendrical coordinates, (r, θ, z). The sphere is centered about the origin, with radius 5, and the drill is radius 4 and drilled parallel to the z-axis, through the origin.

Since the drill has radius 4, and the sphere 5, the "ring" begins when the distance to the origin is equal to 5, and the distance along the r-axis is 4. That forms a right triangle, with a leg of length 4 and a hypotenuse of 5, which implies the other leg is 3. This is the distance along the z-axis above and below the origin that the ring begins and ends. So, z ∈ Z = [-3, 3].

The radius ranges from 4 (the radius of the drill) to 5²=r²+z², or r ∈ R = [4, √25-z²].

There's a third set of limits to consider, which is the limits of the θ-axis, which ranges from θ ∈ Θ = [-π, π].

In cylindrical coordinates, the volume element is dV = r dr dθ dz. So we set up the integral:

V = ∫dV = ∫_Θ ∫_Z ∫_R r dr dθ dz

But since this is only a double-integral, let's get rid of θ...

V = ∫_Θ dθ ∫_Z ∫_R r dr dz = 2π ∫_Z ∫_R r dr dz

[Aranfan]

Okay, that gets me 36pi, which the computer says is correct.

I think I understand what you did there, but why is the angle from -pi to pi?

[Aranfan]

Never mind, I just figured it out.

[Wyrm]

Here's an exercise for you in a similar vein:

Suppose your problem, except that the radius of the drill is a, and the radius of the sphere is b. Prove that the volume of the cored-out sphere to be the same as a sphere with radius h = √b²-a².

[Surlethe]

If you want to use a volumes of rotation method, here's how you set up the integrals.

Option 1: Rotating cylinders.

The basic function here is x2+y2=52, or y=√25-x2. For reasons that Wyrm posted above, we're concerned only with the function above [-3,3]. The surface area of a cylinder is 2πrh, so for a height y above the x-axis, the volume of the associated cylinder of revolution is 2πy(2x)dy. Since x=√25-y2, we have the desired integral: ∫[4,5]4πy√25-y2dy. This can be simplified substantially with a simple change of coordinates.

Option 2: Washers.

As above, we're concerned with y=√25-x2 over [-3,3]. Rotating about the x-axis, the volume of a washer is π(y2-42)dx, so the integral will be ∫[-3,3]π(9-x2)dx.

I get 36π for both methods.

[NomAnor15]

So wait, why do you even have to do this as an integral? It seems to me (unless I'm missing something important) you could just calculate the volume of the original sphere, calculate the volume of the cylinder, and subtract the latter from the former. No integration required. Unless you are specifically told to do it with an integral, then just ignore this.

[Surlethe]

So wait, why do you even have to do this as an integral? It seems to me (unless I'm missing something important) you could just calculate the volume of the original sphere, calculate the volume of the cylinder, and subtract the latter from the former. No integration required. Unless you are specifically told to do it with an integral, then just ignore this.

The hole through the middle is not perfectly cylindrical - you have two little "caps" on top whose volume gets shifted from hole to sphere in this method.

[Narkis]

So wait, why do you even have to do this as an integral? It seems to me (unless I'm missing something important) you could just calculate the volume of the original sphere, calculate the volume of the cylinder, and subtract the latter from the former. No integration required. Unless you are specifically told to do it with an integral, then just ignore this.

The hole through the middle is not perfectly cylindrical - you have two little "caps" on top whose volume gets shifted from hole to sphere in this method.

Unless I'm mistaken, it's relatively easy to calculate the volume of those two little "caps" and subtract them from the sphere too. It should still be easier to do than using integration.

[Surlethe]

How would propose to do that without integrating?

[NomAnor15]

I'm still a little unclear on where these caps are even coming from. If you have a cylindrical drill, and you just drill it straight through the sphere, where are the caps?

[Narkis]

The caps are on the cylinder of air we created in the middle of the sphere.

The equation for the volume of a spherical cap is Vcap=1/6*pi*h*(3r2+h2), where r is the radius of the cap's base and h its height. Now, since we don't know this one's height, we'll use the Pythagorean Theorem, which gives us R2=r2+(R-h)2, where R the sphere's radius.
Plugging in the numbers, and we get 52=42+(5-h)2 => (5-h)2=25-16 => 5-h=√9 => h=2
Back to the first equation, and it becomes V = 1/6*pi*2*(3*42+22) = 1/3*pi*52=17.33pi
The volume of the sphere is Vsph=4/3*pi*53 = 166.67pi
The volume of the cylinder is Vcyl=pi*r2*H, where H the height of the cylinder. H=2*(R-h)=6 So Vcyl=pi*42*6 =96pi
Putting it all together we have Vring=Vsph-Vcyl-2*Vcap=(166.67-96-2*17.33)pi=36.01pi, which would've been exactly 36pi had I stayed with fractions.

So that's the same result, without using any math that a (smart) high school student wouldn't understant.

[NomAnor15]

The caps are on the cylinder of air we created in the middle of the sphere.

Why? I still don't see it. Maybe a picture will help *searches*. This is what I am imagining it as (with a different scale, of course);


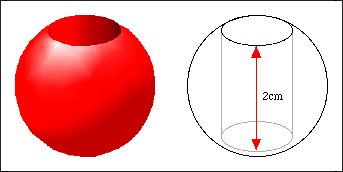
Clearly there are no caps in this picture. What am I missing?

[Steel]

They cylinder you bored out does not have flat ends. Thats what you are missing. The volume of the cylinder is larger than 2pi*rh.



Narkis: Great, and where did you get your expression for the volume of a cap?

Of course its possible to do almost all maths without integrating anything yourself if you just use someone elses integral.

Lets compare the approaches:

Integration:

Line 1: Express problem as integral
Line 2: Answer

Long winded method:

*Look answer up in book*
Fiddle
Manipulate
Fudge geometry
Answer

I think we can see which is superior from both an aesthetic and a computational standpoint...

[Narkis]

The top and bottom of the cylinder in your picture are flat. If we want to make a full sphere out of these pieces, we'll need to "cap" the normal cylinder so that it curves.

Here's a horrible paint image of what I mean: http://img27.imageshack.us/img27/9864/40929718.jpg

edit to answer Steel: It's in my geometry book, but I imagine it can be found with some Google-fu. And I never said my method is faster or more elegant, just easier for someone to use. Chewed food, if you will/

[NomAnor15]

They cylinder you bored out does not have flat ends. Thats what you are missing. The volume of the cylinder is larger than 2pi*rh.

The top and bottom of the cylinder in your picture are flat. If we want to make a full sphere out of these pieces, we'll need to "cap" the normal cylinder so that it curves.

Oh, wow, I am an idiot. I was so focused on the shape left (the ring) that I was totally ignoring the cylinder itself. Fuckin' A, I can't believe I just did that. Thanks for the correction.

[Steel]

edit to answer Steel: It's in my geometry book, but I imagine it can be found with some Google-fu. And I never said my method is faster or more elegant, just easier for someone to use. Chewed food, if you will/

That was kind of my point, that that formula would have been arrived at by doing precisely the integrals done above, and a quick googling will turn up the answer to this problem in its entirety anyway. Once you do a few integrals like this then it becomes quicker than reaching for a textbook.

[Wyrm]

So that's the same result, without using any math that a (smart) high school student wouldn't understant.

Strictly speaking, true. However, the OP said this is a calculus problem. Using your cap formula violates the spirit (and letter) of the problem, and would likely earn him a wrong answer.

Also, those formulae you just used were likely derived from calculus.