Friend wrote: I have a question that plague my mind, and now also the rest of my coworkers at lunch (possibly because I keep bringing it up).
Let us assume two humans, named "A" and "B" as a result of a extremely complex background story we best not get into at this time. What is important is that they are directly beside each other, both standing still.
At one point, A starts to run. Fast. Close to light speed fast. B stands still, watching A with a tired face. B, being a master of the art of Observation, can clearly see A's mechanical watch move slower than normal. A, being well trained in the fine art of Observation himself, notices B's watch picking up speed. This is hereby referred to as "Situation A". Any passing gods would indeed look upon it and claim that this shit looks well.
Lets assume that A returns, stops beside B, informs B that "he's it", and that person B starts running in the exact opposite direction in the exact same speed. The powers that be has named this "Situation B". In Situation B, B's clock would appear for A to be going slowly. This seems a agree-able fact.
My problem is that A & B in both situations have the exact same relative speed to each other. This means that they should observe each other in exactly the same way. But they don't. The person being "slowed" is different, even thou they, relative to each other, are moving in exactly the same way. Why?
Question about relativity.
Moderator: Alyrium Denryle
- The Infidel
- Jedi Master
- Posts: 1343
- Joined: 2009-05-07 01:32pm
- Location: Norway
Question about relativity.
Hi, I have a question from a friend. I think the answer has something to do with time dilation as one approaches c, but I'm not sure, so if any of you know what you're talking about, and I know some of you do, I would really appreciate an answer. 


Where am I at in the post apocalypse draft? When do I start getting picks? Because I want this guy. This guy right here. I will regret not being able to claim the quote, "The first I noticed while burning weed, so I burned it, aiming at its head first. It wriggled for about 10 seconds. Too long... I then fetched an old machete [+LITERALLY ANYTHING]"
- Raw Shark on my slug hunting
- Raw Shark on my slug hunting
Re: Question about relativity.
First of all, his premise above is wrong.B, being a master of the art of Observation, can clearly see A's mechanical watch move slower than normal. A, being well trained in the fine art of Observation himself, notices B's watch picking up speed.
In fact, person A would look at person B's watch and would obverse that watch B is ticking slower than watch A.
Likewise, person B would look at person A's watch and would observe that watch A is ticking slower than watch B.
In both cases, the observer thinks that the other watch is ticking more slowly than his own.
- The Infidel
- Jedi Master
- Posts: 1343
- Joined: 2009-05-07 01:32pm
- Location: Norway
Re: Question about relativity.
Are you sure? I read once that if you had two twins and one took a trip with a spaceship approaching c for a few years (earth time), the twin(spaceship) would be younger than twin(earth) because time went slower for him as he had traveled close to the only static thing in the universe: c in vacuum.


Where am I at in the post apocalypse draft? When do I start getting picks? Because I want this guy. This guy right here. I will regret not being able to claim the quote, "The first I noticed while burning weed, so I burned it, aiming at its head first. It wriggled for about 10 seconds. Too long... I then fetched an old machete [+LITERALLY ANYTHING]"
- Raw Shark on my slug hunting
- Raw Shark on my slug hunting
Re: Question about relativity.
Yes, that is called the Twin Paradox (it's not actually a paradox, though).The Infidel wrote:Are you sure? I read once that if you had two twins and one took a trip with a spaceship approaching c for a few years (earth time), the twin(spaceship) would be younger than twin(earth) because time went slower for him as he had traveled close to the only static thing in the universe: c in vacuum.
But the initial scenario you gave described person B observing person A's watch ticking slowly, while person A observed person B's watch ticking fast. That's the part that's not true. Both people see the other person's watch ticking more slowly than their own. However, the person that ran away will still age less than the person who stayed still. This is why it's referred to as the Twin Paradox, because on this basis it seems like it's a symmetric problem - "if both people see the other's watch ticking slowly, why is it specifically the traveler who ages less?".
Let me re-iterate: no matter which person is the one that accelerated, when two observers have a high relative speed, they both observe the other's watch as ticking too slowly.
This doesn't change the fact that the one who accelerated away will ultimately age more slowly. If I have more time later today I can explain a simplified scenario that shows how the problem is not actually symmetric, and why it is specifically the traveler who ages slowly and not the person who stays still.
- The Infidel
- Jedi Master
- Posts: 1343
- Joined: 2009-05-07 01:32pm
- Location: Norway
Re: Question about relativity.
OK, this baffles me. I feel like I can toss normal logic out the window.Magis wrote: Both people see the other person's watch ticking more slowly than their own. However, the person that ran away will still age less than the person who stayed still.
I can understand this. All movement is relative to something. I thought (in err?) that since c is absolute, if you approach that speed, time will slow down as compared to someone moving slower, even if the relative speeds are the same.Magis wrote: Let me re-iterate: no matter which person is the one that accelerated, when two observers have a high relative speed, they both observe the other's watch as ticking too slowly.
I would really like that. Take your time and answer in you own leisure. I have given my friend a link to this thread, but he's not a member of the board.Magis wrote: This doesn't change the fact that the one who accelerated away will ultimately age more slowly. If I have more time later today I can explain a simplified scenario that shows how the problem is not actually symmetric, and why it is specifically the traveler who ages slowly and not the person who stays still.


Where am I at in the post apocalypse draft? When do I start getting picks? Because I want this guy. This guy right here. I will regret not being able to claim the quote, "The first I noticed while burning weed, so I burned it, aiming at its head first. It wriggled for about 10 seconds. Too long... I then fetched an old machete [+LITERALLY ANYTHING]"
- Raw Shark on my slug hunting
- Raw Shark on my slug hunting
-
Vejut
- Padawan Learner
- Posts: 308
- Joined: 2002-08-28 11:34pm
- Location: edge of hickville, just inside suburbia
Re: Question about relativity.
I believe part of it is that the basic coffee-book relativity is special relativity. It deals with constant speed reference frames. Accelerating frames, like somebody slowing down to turn around and come back, or just turning, need the use of general relativity, which I know very little about beyond the fact that even simple stuff for it needs matrix math...
Magis probably has a more complete and better explaination.
Magis probably has a more complete and better explaination.
- Darth Holbytlan
- Padawan Learner
- Posts: 405
- Joined: 2007-01-18 12:20am
- Location: Portland, Oregon
Re: Question about relativity.
The twins paradox is pure special relativity, which deals fine with acceleration. General relativity is required only once you throw gravity into the mix.
The key point that results in A aging/experiencing time more slowly than B is that A is the one that turns around to meet back up with B, while B stays still. If A had stayed on course after accelerating away and B had decided to accelerate to an even faster velocity to catch up, then B would have aged less than A once B caught up.
I suggest reading the Wikipedia page on the subject. It seems reasonably complete and has several helpful diagrams.
The key point that results in A aging/experiencing time more slowly than B is that A is the one that turns around to meet back up with B, while B stays still. If A had stayed on course after accelerating away and B had decided to accelerate to an even faster velocity to catch up, then B would have aged less than A once B caught up.
I suggest reading the Wikipedia page on the subject. It seems reasonably complete and has several helpful diagrams.
-
Kuroneko II
- Redshirt
- Posts: 7
- Joined: 2013-08-31 06:41pm
Re: Question about relativity.
OK, this baffles me. I feel like I can toss normal logic out the window.[/quote]The Infidel wrote:Both people see the other person's watch ticking more slowly than their own. However, the person that ran away will still age less than the person who stayed still.
It's actually just basic geometry. Let me make an analogy in the ordinary Euclidean plane first.
Suppose there are two people, A and B, that stand on a plane very close to each other, so they are essentially located at the same point. However, they're facing in different directions, and both decide to draw an x-axis is to the right and y-axis to the direction they're facing. So the situation is something like this:
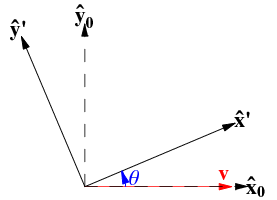
I'm cribbing the diagram from somewhere else. Let's say A's axes are along the x̂₀,ŷ₀ vectors and B's axes are along the x̂,ŷ vectors.
Imagine that both persons absolutely insist on measuring things along those personal axes, calling the length in the x direction width and length in the y-direction depth.
Code: Select all
^y A and B are stand at O, angle θ.
| Person A places a rod of unit length
y' _-|Q along OQ.
\_- | -> A says the rod is has depth OQ = 1.
P\ |
\ | Person B looks at the same rod, but
\ | measures depth along B's own y-axis.
\| -> P is a right angle
O -> B says the rod's depth is OP=cos θ.
Code: Select all
^y
y' | Person B places a rod of unit length
\______| along OP.
P\ |Q -> A says the rod has depth OP = 1.
\ |
\ | Person A looks at same rod, but
\ | says it has length OQ = cos θ.
\ |
\|
OIf you understand the above scenario, you're in good shape to understand time dilation. Instead of a y-axis, suppose we have a t-axis. We're in spacetime, where the history of each object's location at each instant of time traces out a curve, a wordline. For an inertial observer, that worldline is straight, and so can serve as the usual sort of Cartesian coordinate axis. "Facing in a different direction" is analogous to having a different velocity: if an object's wordline is parallel to some observer's t-axis, then it's staying on the same place (same x-coordinate), and in general the slope of some object's worldline, Δx/Δt, is a velocity.
As before, observers measure duration as length along their t-axis, and because they can have non-parallel temporal axes, they each think the other is wrong by exact same factor. The only thing that's really different is that the geometry is pseudo-Euclidean, with angles working a hyperbolically--instead of ordinary cosine (cos), they're related via hyperbolic cosine instead (cosh). The hyperbolic angle between different temporal axes is usually called 'rapidity' in physics, and the hyperbolic cosine of that angle is the Lorentz factor γ.
We can back up a little bit.Magis wrote:This doesn't change the fact that the one who accelerated away will ultimately age more slowly. If I have more time later today I can explain a simplified scenario that shows how the problem is not actually symmetric, and why it is specifically the traveler who ages slowly and not the person who stays still.
-- In Euclidean geometry, straight lines are have give the shortest distance between any two points on them.
-- In special relativity, straight worldlines (zero acceleration) give the longest distance (duration) between any two points (events) on them.
The flip of straight lines from shortest to longest is because of the slightly different geometry (STR's spacetime is pseudo-Euclidean), but those two things are completely analogous. And just like the very intuitive triangle inequality,
-- In Euclidean geometry, if you go from A to C in a straight line, the distance you traverse is shorter than if you make a detour from A to B to C (unless A,B,C collinear).
-- In special relativity, if you go from A to C in a straight line (inertially), the duration you experience is longer than if you make a detour from A to B to C (unless A,B,C collinear).
No, Darth Holbytlan is correct. Special relativity has absolutely no problem dealing with acceleration--it actually would be kind of useless if it couldn't do that.Vejut wrote:I believe part of it is that the basic coffee-book relativity is special relativity. It deals with constant speed reference frames. Accelerating frames, like somebody slowing down to turn around and come back, or just turning, need the use of general relativity, which I know very little about beyond the fact that even simple stuff for it needs matrix math...
- The Infidel
- Jedi Master
- Posts: 1343
- Joined: 2009-05-07 01:32pm
- Location: Norway
Re: Question about relativity.
Wow! Thanks a lot. This will take some time for me to digest and I got a reply from my friend. He just wrote "mind=blown", so I guess he'll read this a few more times as well.
Kuroneko II? Are you the old Kuroneko?
Kuroneko II? Are you the old Kuroneko?


Where am I at in the post apocalypse draft? When do I start getting picks? Because I want this guy. This guy right here. I will regret not being able to claim the quote, "The first I noticed while burning weed, so I burned it, aiming at its head first. It wriggled for about 10 seconds. Too long... I then fetched an old machete [+LITERALLY ANYTHING]"
- Raw Shark on my slug hunting
- Raw Shark on my slug hunting
-
Kuroneko II
- Redshirt
- Posts: 7
- Joined: 2013-08-31 06:41pm
Re: Question about relativity.
If you'd like elaboration on something, don't hesitate to ask. I made an analogy to a completely Euclidean situation to motivate that the "both think the other is wrong by the same factor" situation isn't something mysterious or paradoxical, and it the STR situation is straightforwardly analogous, but there's more interesting things about the geometry in STR.The Infidel wrote:Wow! Thanks a lot. This will take some time for me to digest and I got a reply from my friend. He just wrote "mind=blown", so I guess he'll read this a few more times as well.
In Euclidean geometry, rotation works along circles, i.e., the curves of constant distance from the origin.
In STR, constant-distance (duration) curves are actually hyperbolas, and consequently spacetime rotations (Lorentz boosts) go along hyperbolas.


Euclidean rotation vs spacetime rotation (Lorentz transformation). The asymptotes of the hyperbola represent signals passing through the origin at the speed of light. No matter how how you boost an object's velocity (i.e., hyperbolic angle), it won't go past that asymptote--it won't break the speed of light.
Images stolen from this page, reading which I recommend.
Yes.The Infidel wrote:Kuroneko II? Are you the old Kuroneko?