Tropospheric temperature lapse rate for Earth-like planets

[agent009]

I've been trying to solve a puzzle... dry adiabatic lapse rate is normally calculated as following:

Γ = g·M/cp

where Γ is the lapse rate, g is surface gravity acceleration, M is the mean mole mass of air mixture and cp is its molar heat capacity.

However, if you calculate this for Earth, you arrive at 9.77 K/km, but actual environmental lapse rate, as defined in the ISA, is 6.49 K/km, which is about 9.77 * 0.665. So, I decided to take a look at how this works on Venus and Titan - the only two other worlds in the Sol System that actually have tropospheres.

On Venus (assuming tropopause at 55 km), the average lapse rate is about 7.9 K/km, but the above formula gives you 10.46 K/km, which means that you must multiply the result by 0.756 to get the actual value. On Titan (assuming tropopause at 42 km), actual average lapse rate appears to be around 0.5 K/km, but predicted lapse rate is 1.26 K/km - which gives you the coefficient 0.427. So I've been trying to figure what this mysterious coefficient depends upon - and, I think, I've found it. The following expression gives you almost exactly those numbers (using SI units, that is):

³√(12·g·M·(1/R - 1/cp))

where R is the ideal gas constant. Note, that M·(1/R - 1/cp) is what you must divide the temperature value by to get the square of the speed of sound (I call inverse of this number the "speed of sound factor" because it is constant for any arbitrary gas mixture and gives you the best idea how any changes in atmospheric composition would affect the speed of sound) .

I'm not sure why the heck this works, but the following formula predicts the actual mean tropospheric lapse rates for all 3 worlds with astonishing degree of accuracy:

Γ = (g·M/cp)·³√(12·g·M·(1/R - 1/cp))

For Earth this gives you exactly the standard ISA lapse rate - down to 0.01 K/km precision! For Venus, it predicts the average measured lapse rate with nearly the same degree of accuracy! For Titan, there is somewhat less actual data available and the situation seems to be complicated by the fact that mole fraction of methane apparently varies significantly with altitude, but all measurements reported so far seem to correspond with the result predicted by the above formula at least by order of magnitude.

A coincidence? Well, the lapse rate predicted for Titan (based on 95% N₂ / 5% CH₄ atmospheric composition) would be 0.42 K/km. We'll see if this actually turns out to hold true once more data is available.

[madd0ct0r]

the derivation that gets you the initial equation assumes an atmosphere in hydrostatic equilibrium. It also assumes zero moisture content and the only heat variance coming from a packet of air expanding due to variance in pressure.

the ISA value comes from a 1976 standard. It's very far from a simple linear distribution.


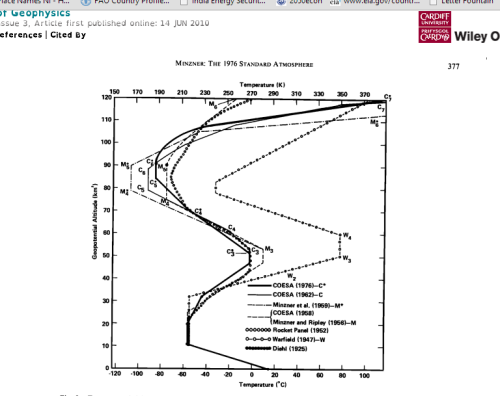
Original paper: http://onlinelibrary.wiley.com/doi/10.1 ... p00375/pdf


The coeffecient relationship you've come up with looks suspiciously like a pseudo 3d-advective diffusion factor. Is it dimensionless?

[Broomstick]

I wish I understood any of that!

Well, of course I know about the lapse rate - required topic in flight school. However, there is was strictly an approximated value and the emphasis was on the empirical, not the theoretical. Actual weather data was usually close but never quite what was predicted.

[agent009]

The coeffecient relationship you've come up with looks suspiciously like a pseudo 3d-advective diffusion factor. Is it dimensionless?

Yes, it is dimensionless. I'm perfectly aware that ISA is just an approximation of more or less sensible mean values, but it's the only reasonable approximation we've got so far.

I'm not quite sure what is the significance of this relationship - I was just looking at ISA and Venus main values and it suddenly struck me that this relation was very close to the relation between the "speed of sound factor". I've played a bit with numbers and it turned that the relation between cubic root of this number and lapse rate was nearly the same. Then I took a look at Titan data, but the relation did not seem to hold. So, I though to myself: "what might Earth and Venus have in common that could matter for lapse rate relation that is very different on Titan?". The obvious answer was g, because otherwise their atmospheres are radically different. So, I tried to introduce g into the equation, and was amazed that, it not only made sense in terms of Titan data, but also got me closer relation between Earth and Venus data - the relation was proportional to nearly the same number. I was even more amazed when I realized that this number was nearly exactly the cube root of 12! And I was completely astonished that, when I rounded it to ³√12, the result for Earth was exactly the ISA lapse rate - with 2 decimal points precision!

[madd0ct0r]

ok. can you talk me through the components then?

³√(12·g·M·(1/R - 1/cp))

g= surface gravity accelration = 9.81 (earth) m s-1-s-1
M= molar mass of dry atomsphere 28.9645 (earth) g/mol (presumably at sea level?)
R= ideal gas constant = 8.314 J K−1 mol−1
cp= ???

[agent009]

g= surface gravity accelration = 9.81 (earth) m s-1-s-1

exactly

M= molar mass of dry atomsphere 28.9645 (earth) g/mol (presumably at sea level?)

kg/mol, if you use standard SI units, which would be 0.0289645 for standard Earth air at MSL

R= ideal gas constant = 8.314 J K−1 mol−1

yep

cp= ???

cp - molar heat capacity under constant pressure in J/mol̇·K (29.115 for Earth air, 29.104 for N₂, 29.378 for O₂ etc.)
cp/M gives you the specific heat capacity under constant pressure in J/kg·K (1005 for Earth air, 1039 for N₂, 918 for O₂ etc.)
cp - R gives you the molar heat capacity under constant volume in J/mol̇·K
(cp - R)/M gives you the specific heat capacity under constant volume in J/kg·K

(p·M)/(R·T) gives you the density for ideal gas in kg/m³.

[agent009]

[duplicate post by accident... could the mods please delete it, since I don't seem to be able to...]

[Broomstick]

Usually it just gets edited it to "duplicate post" and it stays in line - no big deal, no problem. The mods don't usually remove them although of course you can always ask.

[madd0ct0r]

OK, so unpacking: ³√(12·g·M·(1/R - 1/cp))

1/R and 1/cp have matching units and so can be added. inverted units: K.mol.J-1

the 12 is dimensionless and can be neglected

³√(g.M.above) = ³√( (m.s-2).(kg.mol-1).(K.mol.J-1) )

= ³√( (m.s-2).(kg.mol-1).(K.mol.J-1) )
= ³√(m.kg.K.J-1.s-2)

J has si units kg.m2.s-2

= ³√(m.kg.K.kg-1.m-2.s2.s-2)
= ³√(m.kg.K.kg-1.m-2.s2.s-2)
= ³√(m.K.m-2.s2.s-2)
= ³√(m.K.m-2.)
= ³√(K.m-1.)
=K1/3.m-1/3

it's not dimensionless, and so you can't multiply a lapse rate with units K/km to get another lapse rate with units K/km. The number and units you have look suspiciously like the output of an advection process (see the Reynolds Stresses), but since the unit's don't work out, it's not a valid solution.

The original equation you started working with assumes a control volume with a constant M and cp.
Either one of those assumptions don't hold true, or further heat energy is lost from the control volume through another process.

[agent009]

As I said... I do not claim that I completely understand how it works yet. All I know so for that this model seams to work nearly perfectly for Earth and Venus and appears to work reasonably well for Titan, considering scarcity and imprecision of data we have from there so far. Considering there are no other worlds we can study at the moment that actually have a troposphere, I cannot do much better than that for the time being... maybe this factor 12 has some significance that I do not understand yet...

[madd0ct0r]

factors of 12 turn up in all sorts of odd places, normally where integration has been involved.

Unit wise, for your coefficient to work you need something to make that 12 that will resolve to m.K-1, but this is well above my own experience. literally

[agent009]

Yes, it needs to be 12 m/K... so it's gotta be that. I'd be dammed if I knew how at this point