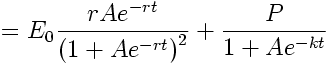Differential Equation Question

[Surlethe]

So, I'm messing around with an elementary differential equation:

As best as I can tell, jury-rigging it a little bit, it turns into this:

where A and B are parameters that depend on E_0 and P, respectively. I'm trying to go for a sum of a logistic distribution and logistic curve, and the graph looks like I want it to, so I'm cautiously optimistic.

My question: is it possible to find a closed-form expression for E_c(t) from this? My knowledge of differential equations is rudimentary at best, and I'm pretty sure the equation isn't separable, so I'm not really sure what to do from here. I'd appreciate some help.

[Kuroneko]

So, I'm messing around with an elementary differential equation:
dE/dt = rE[1-E/E0] + P/[1+Aexp(kt)]
As best as I can tell, jury-rigging it a little bit, it turns into this:
dE/dt [or E?] = E0[rAexp(-rt)]/[1+Aexp(-rt)]² + P/[1+Aexp(-kt)]

If that's E in your second equation, that's definitely not the solution; if it's dE/dt, it's not equivalent to the previous. The first equation almost definitely has no closed-form solution, while the latter is fairly easy: for E(0) = E0,
E(t) = [P/k]log(Δ_k/(1+A)) + [E0 + PΔ_r]/Δ_r + AE0/(1+A), Δ_x = 1+Aexp(-xt).
It's not really an interesting differential equation, since it's just a straight integration problem. I'm not sure what exactly you were doing to go from the first to the second, however, or where the B parameter disappeared to.

[Edit: Δ_k instead of in Δ_r in first term. Gah.]

[Surlethe]

Whoops. That third A in the second equation is supposed to be the B parameter.

first equation almost definitely has no closed-form solution, while the latter is fairly easy: ...

It has no closed-form solution? That's nasty. It seems to translate intuitively to a graph like the logistic curve, but asymptotic to a linear function instead of a constant function. This is math, though, so I've got no business trusting my intuition anyway.

... = 1+Aexp(-xt).

If A depends on E, is that a closed-form solution?

I'm not sure what exactly you were doing to go from the first to the second, however, or where the B parameter disappeared to.

The reasoning I used was that since the first term in the first equation is the derivative of a logistic equation, it should be equivalent to a logistic distribution.

[metavac]

I'm still trying to figure out how you got Eq 2 from 1. I suspect you tried setting k = 0 to get rid of the scaled sigmoid (but I don't know why you'd do that), and then simply plugged in the solution for E_c' = E_c (1 - \frac{E_c}{E_0}), but that doesn't work either. And like kuroneko pointed out, the B parameter's missing.

That said, if P is not constant and P = -Cke^{-kt} then you can use integration by substitution and the solution is closed form.

[metavac]

At times like this, it would be nice to have a port of this for phpBB.

[Kuroneko]

Whoops. That third A in the second equation is supposed to be the B parameter.

Heh. I think I've probably made a sign error in solving it above. Replacing the last one with B, the solution is
E = [P/k]log[Δ_k/(1+B)] + E0[1+2a]/[1+a] + Pt - E0Aexp(-rt)/Δ_r, Δ_r = 1+Aexp(-rt), Δ_k = 1+Bexp(-kt).
(I've checked this one brute-force.)

It has no closed-form solution? That's nasty. It seems to translate intuitively to a graph like the logistic curve, but asymptotic to a linear function instead of a constant function. This is math, though, so I've got no business trusting my intuition anyway.

Which? For large t and r,t positive, the second equation has dE/dt ~ 0. I'm assuming P is constant, since there is no information to indicate otherwise. The first one should eventually have dE/dt ~ 0 as well.

If A depends on E, is that a closed-form solution?

No, but it is if A depends on E_0 and E_0 stays constant (that's what I've read your initial post as)...

The reasoning I used was that since the first term in the first equation is the derivative of a logistic equation, it should be equivalent to a logistic distribution.

Sounds like you're misapplying the principle of superposition.

[Surlethe]

Whoops. That third A in the second equation is supposed to be the B parameter.

Heh. I think I've probably made a sign error in solving it above. Replacing the last one with B, the solution is
E = [P/k]log[Δ_k/(1+B)] + E0[1+2a]/[1+a] + Pt - E0Aexp(-rt)/Δ_r, Δ_r = 1+Aexp(-rt), Δ_k = 1+Bexp(-kt).
(I've checked this one brute-force.)

Okay.

It has no closed-form solution? That's nasty. It seems to translate intuitively to a graph like the logistic curve, but asymptotic to a linear function instead of a constant function. This is math, though, so I've got no business trusting my intuition anyway.

Which?

Forgive my ambiguity. I meant the graph of E itself.

For large t and r,t positive, the second equation has dE/dt ~ 0. I'm assuming P is constant, since there is no information to indicate otherwise. The first one should eventually have dE/dt ~ 0 as well.

Are you certain? I suppose I should mention constraints: E tends to E0 as t goes to infinity. So, in the first equation, the first term goes to zero, while the denominator in the second term goes to 1 and the numerator is indeed constant, so the second term goes to P. Same thing happens in the second equation: Aexp(-rt) goes to zero in the numerator of the first term, while the denominator goes to one; the second term goes to P. If my brain's working, then, dE/dt ~ P in both equations.

So, I'm thinking that E will tend asymptotically toward the line Pt + E0.

If A depends on E, is that a closed-form solution?

No, but it is if A depends on E_0 and E_0 stays constant (that's what I've read your initial post as)...

Goddamn it. I can't seem to make up my mind on anything tonight. Let's see. You're right, and I was right, at first.

The reasoning I used was that since the first term in the first equation is the derivative of a logistic equation, it should be equivalent to a logistic distribution.

Sounds like you're misapplying the principle of superposition.

What's that?

[metavac]

What's that?

You solved for E_c naively thinking that it would be in the form of \frac{1}{1 - Ae^{-kt}}. The presence of the sigmoid on the left side screws that up.

[metavac]

Ghetto edit: right side.

[Surlethe]

What's that?

You solved for E_c naively thinking that it would be in the form of \frac{1}{1 - Ae^{-kt}}. The presence of the sigmoid on the left side screws that up.

What do you mean by that? I simply tried -- operative word there -- to make use of the fact that rE(1-E/E0) is an equation for a logistic distribution. Isn't that true?

EDIT: I'm going to go home and sleep on this, then hopefully present the problem a little more coherently in the morning.

[metavac]

What do you mean by that? I simply tried -- operative word there -- to make use of the fact that rE(1-E/E0) is an equation for a logistic distribution. Isn't that true?

Yes, that's true. But your first equation means that E_c yields a sigmoid as a term in its derivative. That means when you go back to substitute a solution to E_c to give you the second equation, you have the sigmoid to deal with. I assumed that's what you were doing, but now I'm not sure.

EDIT: I'm going to go home and sleep on this, then hopefully present the problem a little more coherently in the morning.

I'll try to sober up by then.

[Kuroneko]

I'm going to go home and sleep on this, then hopefully present the problem a little more coherently in the morning.

Yes. It seems I should be sleeping as well (I've had only two hours last night... isomnia is not nice). However, you're only right if you get rid of the above condition.

Are you certain? I suppose I should mention constraints: E tends to E0 as t goes to infinity.

Hmm...

If my brain's working, then, dE/dt ~ P in both equations. ...

The very strange thing about this situation is that whereas we made different assumptions about E0,P,etc., and reached different conclusions, my conclusion is correct under your assumptions and your conclusion is correct under my assumptions (at least for the second equation--the first is different).

So, I'm thinking that E will tend asymptotically toward the line Pt + E0.

That's contradictory. E→E0 as t→∞ forces P→0.

What's that?

For homogeneous linear differential equations, linear combinations of solutions are themselves solutions. It seemed like you were trying to do the reverse for this case--that the first term gives you a solution in a certain form, so you were trying to massage the first term with it. At least, that's what it looked like--I admit I'm at a loss as to how exactly you got from the first to the second.

[Kuroneko]

Hmm... I think I may be beginning to understand what you're trying to do. In the OP, there was no information as to what P was, for example--and that's why both I and metavac were rather confused as to where your second equation came from. Now, I'm still not quite sure how you got it, but the following may be similar to what I'm guessing you're trying to do.

Given a solution P to the initial value problem
[1] dP/dt = kP(1-P/B), P(0) = P0,
find the solution to
[2] dE/dt = rE[1-E/A] + P/(1+Cexp(-kt)), E(0) = E0.

The first equation gives P = B/[1+p.exp(-kt)], p = (B-P0)/P0. If C = p, then
[3] dE/dt = rE[1-E/A] + B/[1+Cexp(-kt)]².
Unfortunately, even in the case of C=p, I doubt that anything but a series solution is possible. This system will still tend to a constant value [Ar + sqrtΖ]/(2r), Ζ = Ar[Ar+4B].

(Alright... now I really need sleep.)

[Surlethe]

Okay, here's a better presentation of the problem, and it should become clear where the variables are coming from. There exists some linear function E_a(t) = E_0 + Pt, with constants E_0, P > 0, that defines the amount of available energy in a given location*. Find the total consumption function E_c. Essentially, it's a generalization of a logistic curve.

Two observations: the consumption will increase exponentially at first, but then it will "level off" and become linear and asymptotic to E_a, so:
[1] E_c < E_a for all t,
[2] E_c ~ E_a, and
[3] dE_c/dt ~ dE_a/dt = P, which follows from [2], I believe, under the assumption that both E_c and E_a are differentiable.

I had initially thought dE_c/dt = rE_c(1-E_c/E_a) would work, since it seems to be an appropriate adaptation of the logistic equation at first glance, but as t goes to inf, this goes to 0 instead of P. so it doesn't meet [3]. Then I got to thinking about what was going on in energy consumption, and I figured, interpret E_0 as the amount of initial energy stored in the system and P as the rate of energy injection into the system. Then these two statements should hold: (1) the total consumption of E_0 should follow a logistic curve, and (2) the rate of change of consumption of energy injected to the system after a time t_0 should follow a logistic curve. I thus settled on a basic format for the equation:

[4] C = dE_c/dt = α(E_0) + β(P),

where α is a logistic distribution based on E_0 and β is an honest-to-god logistic curve asymptotic to P. That's what I was getting at in my questions in the OP, although they seem to be riddled with typos and errors.

* Or, you could just as easily say this is a location with a linearly increasing carrying capacity; find the population curve. Same math.

[Surlethe]

What do you mean by that? I simply tried -- operative word there -- to make use of the fact that rE(1-E/E0) is an equation for a logistic distribution. Isn't that true?

Yes, that's true. But your first equation means that E_c yields a sigmoid as a term in its derivative. That means when you go back to substitute a solution to E_c to give you the second equation, you have the sigmoid to deal with. I assumed that's what you were doing, but now I'm not sure.

Ah, I see. Yeah, I screwed that up by making it dependent on E_c instead of some proportion of E_c, but shouldn't it still hold if I switch from E_c to some parameter E_1?

[Kuroneko]

There exists some linear function E_a(t) = E_0 + Pt, with constants E_0, P > 0, that defines the amount of available energy in a given location*. Find the total consumption function E_c. Essentially, it's a generalization of a logistic curve.

Two observations: the consumption will increase exponentially at first, but then it will "level off" and become linear and asymptotic to E_a, so:
[1] E_c < E_a for all t,
[2] E_c ~ E_a, and
[3] dE_c/dt ~ dE_a/dt = P, which follows from [2], I believe, under the assumption that both E_c and E_a are differentiable.

The hyperbola is probably the simplest curve that meets all three conditions.

I had initially thought dE_c/dt = rE_c(1-E_c/E_a) would work, since it seems to be an appropriate adaptation of the logistic equation at first glance, but as t goes to inf, this goes to 0 instead of P. so it doesn't meet [3].

Hmm? If we take E0 = 0 for simplicity, and based on the logistic function take the ansatz E = exp(rt)/[A - BF(t)], we have [1/rE][dE/dt] = 1 + [BF'(t)]/[rA-rBF(t)] = 1 - E/Pt, and therefore substitution gives [PB/r]F' = -exp(rt)/t. Thus F is essentially the exponential integral function E1; some fiddling gives E = Pexp(rt)/[CP - rE1(-rt)] and C is a constant. One can translate this to get a solution for E0 > 0. However, it doesn't seem to be defined for t>t_c for some negative t_c>-1/2.

[metavac]

Ah, I see. Yeah, I screwed that up by making it dependent on E_c instead of some proportion of E_c, but shouldn't it still hold if I switch from E_c to some parameter E_1?

Replacing E_c on the right side of the equation with some parameter E_1 (I'm assuming one whose t derivative vanishes) leaves us with the sigmoid to integrate, and that function definitely doesn't have a closed-form anti-derivative.

[Surlethe]

The hyperbola is probably the simplest curve that meets all three conditions.

Except that a hyperbola isn't approximately exponential for t close to 0, right?

Hmm? If we take E0 = 0 for simplicity, and based on the logistic function take the ansatz E = exp(rt)/[A - BF(t)], we have [1/rE][dE/dt] = 1 + [BF'(t)]/[rA-rBF(t)] ...

Isn't [1/rE][dE/dt] = 1 - [BF']/[rA-rBF] ?
[1/rE][dE/dt] = [1/rE][d/dt][exp{rt}/(A+BF)]
= [1/rE][{(A+BF)rexp{rt}-exp{rt}BF'}/(A+BF^2)]
= {r(A+BF)-BF'}/{r(A+BF)}
= 1 - BF'/(rA+rBF).

... = 1 - E/Pt, and therefore substitution gives [PB/r]F' = -exp(rt)/t. Thus F is essentially the exponential integral function E1; some fiddling gives E = Pexp(rt)/[CP - rE1(-rt)] and C is a constant. One can translate this to get a solution for E0 > 0. However, it doesn't seem to be defined for t>t_c for some negative t_c>-1/2.

I think I follow what you're doing, though I'm not familiar with E1. But if the sign change carries, then you should get E = Pexp(rt)/[CP + rE1(-rt)]. Does that fix domain problems?

[Surlethe]

Ah, I see. Yeah, I screwed that up by making it dependent on E_c instead of some proportion of E_c, but shouldn't it still hold if I switch from E_c to some parameter E_1?

Replacing E_c on the right side of the equation with some parameter E_1 (I'm assuming one whose t derivative vanishes) leaves us with the sigmoid to integrate, and that function definitely doesn't have a closed-form anti-derivative.

Yes, E_1's t-derivative would vanish. But I'm not talking about finding a closed form for C with E_1 replacing E_c; I'm talking about replacing rE1(1-E1/E0) with the expression for a logistic distribution.

[Kuroneko]

Except that a hyperbola isn't approximately exponential for t close to 0, right?

Heh, yes. That'd be the 0th condition.

Isn't [1/rE][dE/dt] = 1 - [BF']/[rA-rBF] ?

Hmm... no. [1/rE][dE/dt] = 1 + [BF']/[r(A-BF)].

[1/rE][dE/dt] = [1/rE][d/dt][exp{rt}/(A-BF)]
= [1/rE][{(A-BF)rexp{rt}+exp{rt}BF'}/(A-BF)^2]
= ...
= 1 + BF'/(rA-rBF).

We're working with a slightly different ansatz. The post above was E = exp(rt)/[A - BF(t)]. If you change the ansatz to have a different sign of B, the final answer won't be changed, but the intermediate steps will be.

I think I follow what you're doing, though I'm not familiar with E1. But if the sign change carries, then you should get E = Pexp(rt)/[CP + rE1(-rt)]. Does that fix domain problems?

Well, we can actually make this both a bit simpler and more general. Let E be described by the differential equation dE/dt = rE[1-E/f], f = f(t)>0 carrying capacity, and r>0 constant.

Consider the ansatz E = exp(rt)/F, F = F(t), which is sufficiently general, since every non-negative function can be written in this form. Thus, [1/rE][dE/dt] = 1 - [1/r][F'/F], which gives F' = r.exp(rt)/f. Thus, our general solution is E = exp(rt)/[C+r.Int{t₀,t}[ exp(rt)/f dt ] for some constants C,t₀. If we don't try to fix t₀ as ±∞, we actually won't have domain problems for well-behaved f's.

Supposing f is subexponential (or in general, F increases without bound), then in the limit t→∞, E = exp(rt)/F = rexp(rt)/F' = f. Hence if E and f have the same limits as t→∞. Furthermore, in the same limit, E/f = exp(rt)/[Ff] = [r.exp(rt)]/[F'f + Ff'] = 1/[1+f'/(rE)] = 1 if f does not grow too fast (in particular, if f' is bounded).